¿Conoces estos conceptos básicos sobre la Regresión Lineal?
En el mundo de la gestión de carteras y los derivados financieros, es crucial comprender cómo se relacionan los movimientos de diferentes activos entre sí. A través del cálculo de las betas, podemos determinar los ratios de cobertura necesarios para una gestión de riesgos efectiva. Este artículo explorará los fundamentos de la regresión lineal, una herramienta esencial para establecer patrones de movimiento entre activos.
Conceptos Básicos de la Regresión Lineal
Uno de los principales objetivos de la regresión es estimar una variable (variable dependiente) en función de otra (variable independiente). Si estimamos Y en función de x por medio de una ecuación, ésta se denomina ecuación de regresión.
Regresión lineal: Cuando existe relación entre dos variables y podemos expresar esa relación en términos de una aproximación lineal (una recta que representa la relación entre las dos variables):
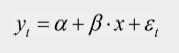
Y es la variable que queremos predecir.
x es la variable que usamos para hacer la predicción.
a es el punto donde la línea intercepta el eje Y.
b es la pendiente de la línea (indicando cómo cambia Y en relación con X), y
e es el error del modelo.
La Regresión Lineal y el Método de Mínimos Cuadrados Ordinarios (MCO)
Uno de los métodos que se suele utilizar para la inferencia es el MCO (mínimos cuadrados ordinarios). Con este método, se representa la nube de puntos (valores reales) y, dibujando las infinitas rectas que pasan por el plano XY, hayamos la distancia de cada valor real a cada recta posible.
Si sumamos todas esas distancias (elevadas al cuadrado para que no se compensen positivas con negativas) existirá una recta que minimiza todas esas distancias al cuadrado. Esta aproximación lineal implica que para cada par de puntos existe un error e, que será exactamente la diferencia con respecto a la recta de regresión Y que se intentará minimizar.
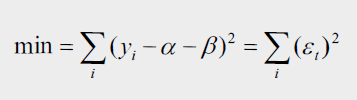
Aplicando las condiciones de minimización llegamos a las siguientes expresiones:

Fiabilidad de las Estimaciones
La fiabilidad de las estimaciones obtenidas a través de la regresión lineal y el método MCO depende de varios factores. Estos incluyen la calidad y cantidad de los datos, la linealidad de la relación entre las variables y la ausencia de problemas estadísticos como la multicolinealidad, heteroscedasticidad o autocorrelación.
Para evaluar la fiabilidad, los estadísticos utilizan diversas métricas, como el coeficiente de bondad de ajuste, el cual indica cómo de bien representa la recta de regresión al conjunto de datos. Es un valor entre 0 y 1, siendo 1 el ajuste perfecto (100%) y 0 el peor ajuste. El objetivo final es averiguar si la recta de regresión es representativa o no (es decir, saber la fiabilidad de los datos para realizar estimaciones).
Tener una base sólida en estadística es fundamental para poder avanzar en el mundo financiero, por ello te invitamos a inscribirte en el curso de Estadística Básica, con el que aprenderás a calcular la volatilidad de una cartera, la correlación entre activos y la regresión lineal para que tú mismo puedas realizar los cálculos y seguir correctamente el resto de cursos.
Descubre el curso Estadística Básica con Enrique Castellanos
Iníciate en nuestra categoría de Mercados y Productos con el curso de Estadística Básica, con el que aprenderás a calcular la volatilidad de una cartera, la correlación entre activos y la regresión lineal.


