¿Utilizas el clustering jerárquico para diversificar tu cartera?
Uno de los principios básicos en la diversificación de carteras consiste en la elección de activos que no estén correlacionados. Por eso, la matriz de covarianzas de los retornos de nuestro universo es un elemento de entrada para procesos de optimización de carteras, trading algorítmico y control de riesgos, entre otros.
Sin embargo, en ocasiones estas decisiones se complementan con una parte cualitativa que involucra un análisis exploratorio de los elementos de entrada. La dificultad surge cuando debido a un número relevante de activos, la matriz de covarianzas no es interpretable de forma sencilla.
Aquí mostraremos con un ejemplo práctico cómo utilizar dendogramas, una herramienta gráfica del clustering jerárquico, para facilitar esta tarea de análisis e interpretación.
Si tuviéramos que elegir un conjunto diversificado de acciones entre los componentes de un índice amplio de mercado, una selección manual de activos de diferentes sectores ya nos arrojaría una solución aceptable.
Ejemplo práctico:
Para hacer nuestro ejemplo más interesante, vamos a proponernos explorar las alternativas de diversificación dentro de un mismo sector, que a priori parece menos evidente.
Partimos del Stoxx Europe 600 Oil & Gas, cuyos componentes podemos encontrar fácilmente a partir de la cesta de algún ETF que replique físicamente este índice sectorial.
Este índice sectorial contiene las empresas del Stoxx 600 que pertenecen o están relacionadas con el sector del petróleo o el gas natural como se puede apreciar a continuación:
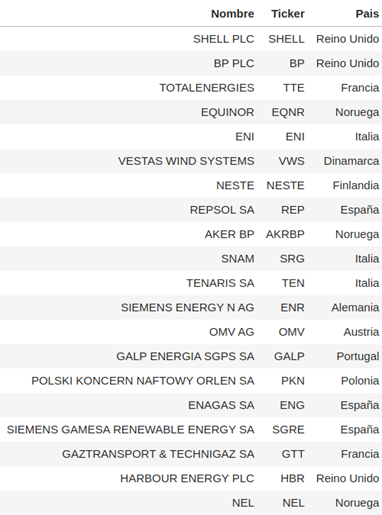
Matriz de correlaciones:
Una estrategia intermedia para facilitar la interpretación consiste en utilizar la matriz de correlaciones, que corresponde a una versión estandarizada de la matriz de covarianzas.
Su construcción es similar: a partir de la serie de precios, se calculan los rendimientos logarítmicos, y para cada par de series de rendimientos se calcula correlación que corresponde a una entrada en la matriz.
Con un rango de [-1, 1] podemos ver los activos más correlacionados con valores más próximos a 1, como muestra la siguiente tabla:
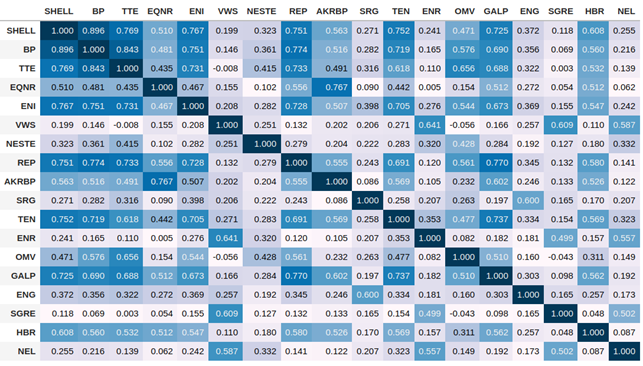
Construcción del dendograma:
El clustering jerárquico es una técnica de machine learning no supervisado que a partir de la similitud entre los elementos del conjunto de datos busca construir una jerarquía de grupos.
Intuitivamente para nuestro ejemplo, esto consiste en que dos acciones muy correlacionadas pasan a formar un grupo, que a su vez puede emparejarse con otros elementos o grupos pero a un nivel más alto de la jerarquía.
Un dendograma es la representación gráfica en forma de árbol invertido y donde elementos unidos más abajo indican mayor similitud y a medida que se enlazan más arriba indican menor semejanza.
Merece la pena aclarar que aunque (1 – correlación) puede utilizarse como medida de similitud, el algoritmo en realidad lo que hace es calcular la similitud a partir de la suma de las diferencias de cuadrados de las correlaciones con el resto de activos (esto es, el cálculo del cuadrado de la distancia euclídea por cada par de filas de la matriz de correlaciones).
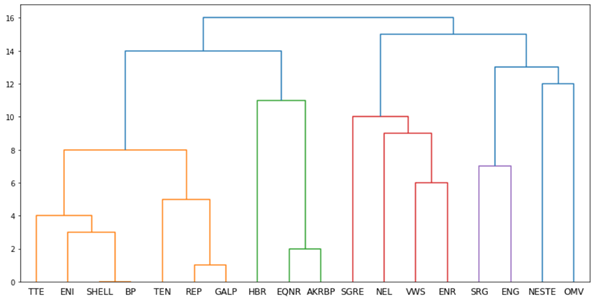
En la figura vemos el dendograma correspondiente a nuestro ejemplo construido fácilmente con Python utilizando las librerías scipy y sklearn.
Interpretación:
Interpretándolo con la altura de los enlaces vemos que (0) Shell y BP tienen la mayor correlación, luego (1) Repsol y Galp, y después (2) Equinor y Akerbp. Sin embargo, todas ellas están completamente alejadas de Neste, que solo se relaciona con ellas en el nivel superior de la jerarquía.
Estas jerarquías nos permiten además determinar grupos separados de elementos. Si trazamos un corte horizontal imaginario entre las alturas 12 y 13 observamos que nos quedaríamos con 5 grupos de acciones que corresponden a los diferentes colores del diagrama.
Una selección manual que esté diversificada se puede hacer eligiendo un elemento de cada uno de estos grupos. Por otro lado, los grupos con enlaces a niveles más bajos están más cohesionados que otros grupos cuyos primeros enlaces aparecen a mayor altura.
Si te interesa profundizar en tus competencias sobre Machine Learning, aquí en Braindex tenemos un curso que presenta una visión general de las técnicas supervisadas y no supervisadas, y entre las no supervisadas vemos el clustering jerárquico de forma similar a como lo hemos discutido en este ejemplo.
Descubre el curso de Machine Learning con Tomás de la Rosa
Iníciate en nuestra categoría de Tecnología con el curso de Machine Learning, con el que te acercarás al Machine Learning con ejemplos del mundo financiero para que puedas entenderlo fácilmente.


