¿Conoces las implicaciones que tiene la volatilidad?
En este artículo aprenderás a interpretar la volatilidad con casos prácticos para conseguir invertir con éxito. El rendimiento de una inversión está condicionado en gran medida por el precio de compra y de venta de los activos que la componen. En este sentido, parece interesante poder cuantificar la variabilidad histórica del precio de estos activos. Así, la varianza de una serie de datos nos indica cómo están de concentrados o dispersos los valores alrededor de su media. Se calcula como la media del cuadrado de las desviaciones respecto a su media (la diferencia entre cada valor y su media se eleva al cuadrado para evitar que una desviación positiva se compense con una negativa). Se suele denominar momento de orden dos (por ser al cuadrado) mientras que la media es el momento de orden uno.
En series financieras en las que se parte de los rendimientos del precio de un activo, la varianza viene expresada en puntos porcentuales al cuadrado, algo difícilmente interpretable. Por eso se trabaja con la desviación típica (la raíz cuadrada de la varianza) que está expresada directamente en porcentaje.
Esta desviación típica (también llamada desviación estándar) suele usarse como medida de Volatilidad (s), aunque también haya otras medidas.
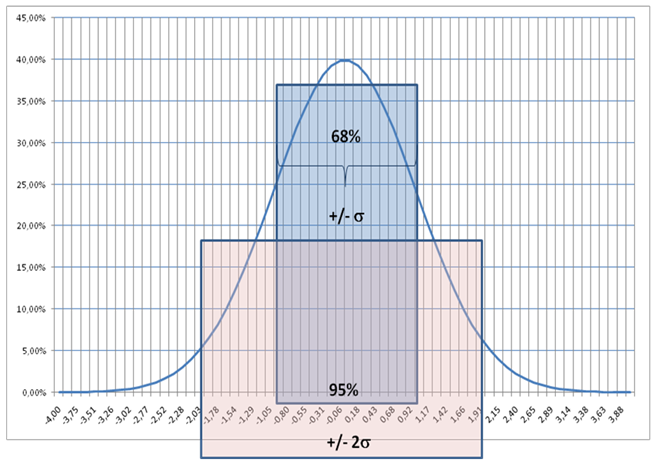
Con respecto a su interpretación, la volatilidad nos informa de la probabilidad de que el rendimiento de un activo se sitúe en determinados intervalos. Así, en una distribución normal la variable aleatoria tiene:
- El 68% de los valores dentro del intervalo +/- 1 desviación estándar (σ)
- El 95% de los valores dentro del intervalo +/- 2 desviaciones estándar (2σ)
- El 99% de los valores dentro del intervalo +/- 3 desviación estándar (3σ)
Gráfico 1: Distribución Normal
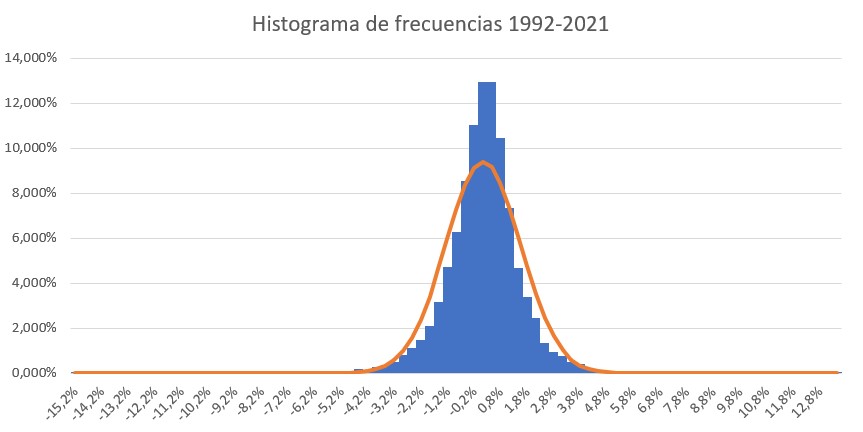
Dicho lo anterior, es importante destacar que la no-normalidad de las distribuciones es habitual en las series financieras. Así, se identifica habitualmente exceso de kurtosis (“colas gordas”/”fat tails” o una mayor probabilidad de que ocurran rendimientos extremos) y asimetría o skewness (hay asimetría negativa, si la “cola” a la izquierda de la media es más larga que la de la derecha, es decir, si hay valores más separados de la media a la izquierda) tal y como se puede apreciar en el gráfico 2.
Gráfico 2: Comparación entre la distribución normal y el IBEX 35 ® desde 1992 hasta Noviembre 2021.
El cálculo de la volatilidad a partir de los rendimientos históricos es la base para la correcta estimación de la volatilidad futura, componente fundamental en:
- Gestión de riesgo, por ejemplo, con metodologías VaR.
- Análisis de resultados ajustados al riesgo y estimación de fronteras eficientes.
- Valoración de instrumentos derivados
- Trading de volatilidad.
Para medir la volatilidad, es necesario que la media de la variable sea estable (estacionaria). Para evitar el efecto de la tendencia, la volatilidad no se calcula directamente a partir de los precios sino de los rendimientos. Dichos rendimientos pueden ser calculados de forma discreta (tomado primeras diferencias) o continua (tomando logaritmos):
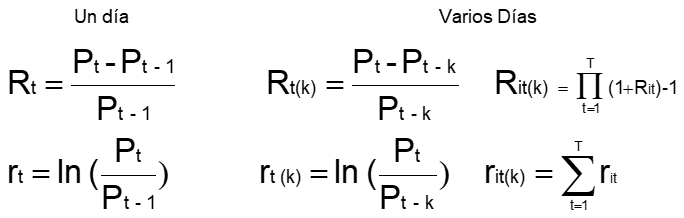
Habitualmente se utiliza el cálculo a partir de los logaritmos (a efectos prácticos, salvo en rendimientos muy grandes, las diferencias son pequeñas) aunque no replique exactamente el mundo real ya que no hay ningún activo que genere un rendimiento continuo. Sin embargo esta formulación es muy cómoda, puesto que tiene propiedades interesantes como por ejemplo que el rendimiento de un período sea igual a la suma del rendimiento de los subperiodos que lo componen.
La volatilidad tiene características especiales, entre las cuales podemos destacar:
- Persistencia.- También conocida como el efecto “memoria”. Se manifiesta en la autocorrelación.
- Clusters.- Los días de altos/bajos rendimientos tienden a estar agrupados.
- Asimetría.- El impacto de los retornos sobre la volatilidad es más fuerte en mercados bajistas que alcistas. Se pone de manifiesto especialmente en los mercados de renta variable.
- Reversión a la media.- Esta característica es algo discutible, o por lo menos matizable. Robert Engle (premio nobel 2003) incorporó esta característica en su modelo ARCH, ya que la experiencia indicaba que las volatilidades suelen revertir a la volatilidad a largo plazo (incondicional). Veremos este modelo en un artículo posterior.
“Para transformar la volatilidad referida a un período y expresarla en otro distinto se utiliza la √T”
La volatilidad se suele expresar en términos anuales, pero se puede calcular a partir de rendimientos diarios, semanales o mensuales.
Así, teniendo la volatilidad diaria (obtenida a partir de rendimientos diarios) podemos expresarla en volatilidad a semanal, mensual o anual multiplicando por la √T. Del mismo modo, si tenemos una volatilidad anual también podemos pasarla a términos diarios, semanales o mensuales dividiendo por la √T.
Pongamos un ejemplo:
IBEX 35® = 11200 y la volatilidad anual es de 28%. Eso significa que:
- Dentro de un año el activo, con una probabilidad de un 68%, estará entre 14336 y 8064 puntos. σ=11200 x 0,28=3136.
- Dentro de un año el activo, con una probabilidad de un 95%, estará entre 17472 y 4928 puntos. 2σ=11200 x 0,28 x 2=6272.
- Dentro de un año el activo, con una probabilidad de un 99%, estará entre 20608 y 1792 puntos. 3σ=11200 x 0,28 x 3=9408.
Como puedes observar, debido a la amplitud del período considerado no es muy útil trabajar con volatilidades anuales. Además, esa volatilidad no es constante (de hecho, es muy inestable) y la predicción no será en absoluto fiable. Si replicamos estos cálculos con datos diarios:
- Mañana el activo, con una probabilidad de un 68%, estará entre 11398 y 11002 puntos.
σ=11200 x 0,28/raíz(252)=197,55. - Mañana el activo, con una probabilidad de un 95%, estará entre 11595 y 10805 puntos.
2σ=11200 x 0,28/raíz(252) x 2=395,10. - Mañana el activo, con una probabilidad de un 99%, estará entre 11793 y 10607 puntos.
3σ=11200 x 0,28 x 3=592,65.
Por lo tanto, trabajar con datos diarios acota más las posibilidades. Obsérvese que hemos dividido la volatilidad anual entre la raíz cuadrada de 252, ya que hay aproximadamente 252 días hábiles (de mercado) en el año. Para facilitar la transformación de las volatilidades anuales en diarias, es muy normal que los traders utilicen la raíz de 256, también llamada regla del 16, de manera que en vez de dividir entre la raíz de 252 (que es 15,87) dividen por la raíz de 256 (que es 16):
| Volatilidad Anual | Volatilidad Diaria |
| 16% | 1% |
| 24% | 1,5% |
| 32% | 2% |
| 40% | 2,5% |
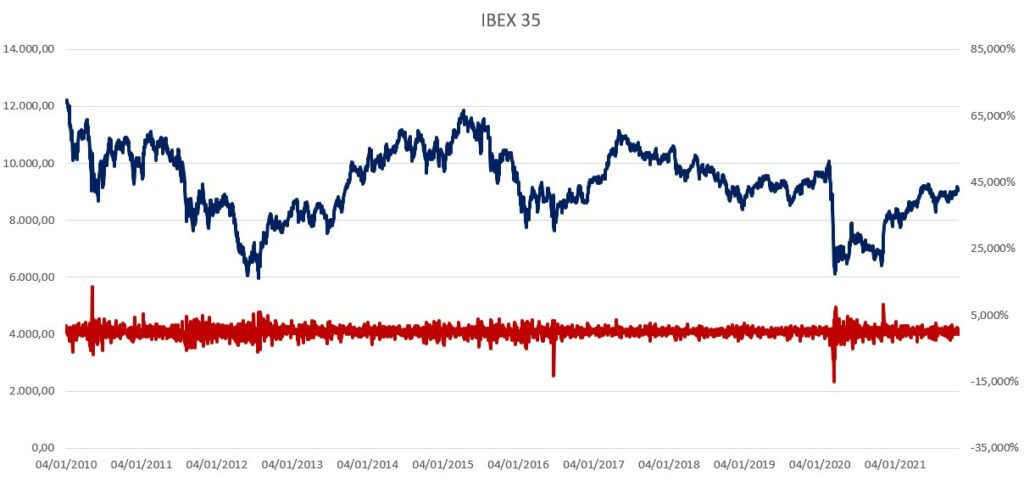
Como podemos ver en el gráfico 3, los rendimientos no son constantes, sino que van variando a lo largo del tiempo. Hay momentos donde los rendimientos son muy altos durante un periodo seguido y momentos dónde los rendimientos son bajos también durante un periodo de tiempo prolongado. Se pueden observar las características antes mencionadas como los clusters, la persistencia y la asimetría.
Gráfico 3: el IBEX 35 ® (eje izdo.) y sus rendimientos (eje dcho.) desde 2010 hasta noviembre 2021.
Conclusiones:
-La volatilidad es la medida de la desviación de los rendimientos con respecto a la media. Se suele calcular con la desviación típica.
-La volatilidad se expresa en términos anuales y para pasarla a datos diarios, semanales o mensuales se utiliza la raíz(t).
-La volatilidad va cambiando, no permanece estable. Los rendimientos altos se generan por un “shock” de mercado y permanecen durante cierto tiempo hasta que se olvida.
-La volatilidad es asimétrica, cuando suben los mercados baja y cuando éstos bajan sube.
Si eres un trader con conocimientos sólidos pero quieres tener en cuenta en tus estrategias la volatilidad, sabiéndola interpretar y calcular para así poder llegar a obtener mejor resultados, te invitamos a complementar tus conocimientos con el curso de Volatilidad, impartido por Enrique Castellanos, Director de Instituto BME.
Descubre el curso de Volatilidad con Enrique Castellanos
Iníciate en nuestra categoría de Mercados y Productos Financieros con el curso de Volatilidad, con el que aprenderás las particularidades de la volatilidad, cómo calcularla y que implicaciones tiene para ayudar en la toma de decisiones.